4.1, 4.2, 4.4, 4.5, 4.6, 4.9, 4.12, 4.14, 4.17, 4.19, 4.22, 4.27, 4.30

4.1

a) Explanatory Variable: amount of time studying
Response Variable: grade on exam

b) Explore the relationship

c) Explanatory Variable: inches of rain in growing season
Response Variable: yield of corn

d) Explore the relationship

e) Explanatory Variable: family income
Response Variable: years of education completed by eldest child

4.2 The explanatory variable is water temperature and the response variable is weight gain of the coral. In this case, the water temperature would be categorical and the weight gain quantitative.

4.4

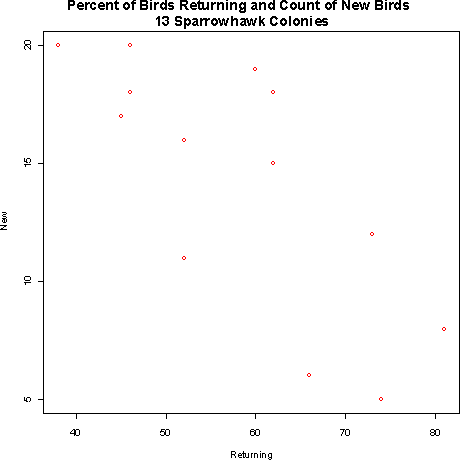
4.5 The relationship between the number of new sparrowhawks and the percentage of returning birds looks like it is linear, moderately strong, and negative. Based on the information given, the sparrowhawk appears to be a longer lived territorial bird.

4.6

a)

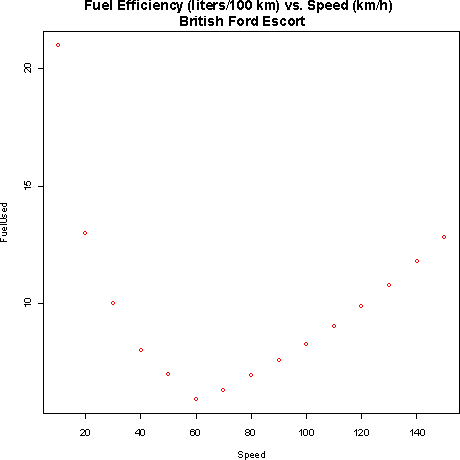
The explanatory variable is speed.

b) Fuel consumption decreases as the speed increases from 0 to 60 then it starts increase again. This makes sense because a certain amount of fuel must be used just to keep the car running. At slow speeds it takes much longer to go a given distance. Much of the fuel use at these speeds is from keeping the car running for that time. As speed increases beyond the optimal point, wind resistance gets stronger and stronger, so the increasing amount of gas required to keep the car going so fast gets to the point where it is far more significant than the reduction due to less driving time.

c) There is negative association between speed and fuel consumption for low speeds and positive association for high speeds. Therefore it would be incorrect to say that speed and fuel consumption were just positively or negatively associated.

d) The relationship looks quite strong. It is easy to see how a smooth curve would pass through all the points.

4.9

a) The correlation between the percent of returning birds and the number of new birds is -.7485.

b)

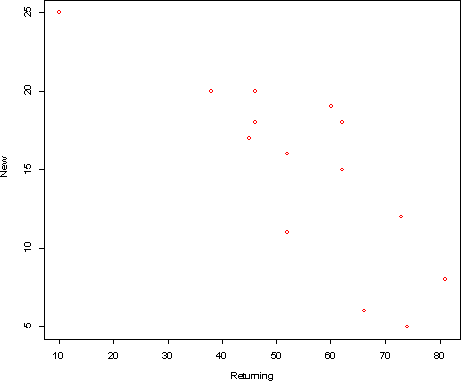
The new correlation with point (10,25) added is -.807

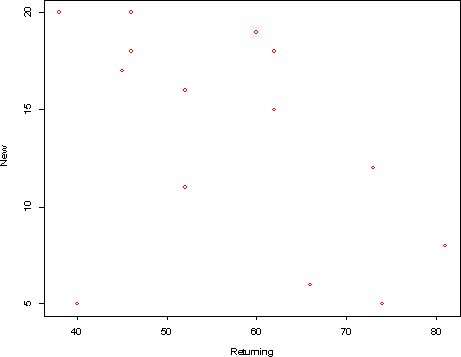
The new correlation with point (40, 5) added is -0.469

c) The point (10,25) lies along the same trend line as the original data, so it tends to strengthen the linear relationship, that is make the correlation stronger. The point (40,5) lies outside the trend line of the original data, so it tends to weaken the linear relationship.

4.12

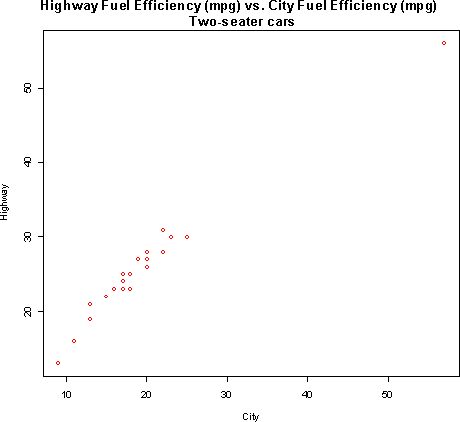
There appears to be a strong linear relationship between fuel efficiency in the city and fuel efficiency on the highway. The Honda Insight is an outlier that extends the pattern shown by the other cars.

4.14

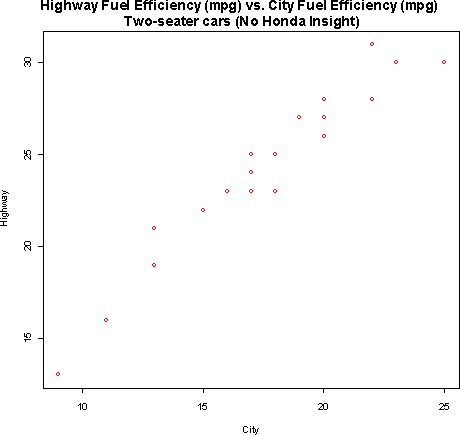
The correlation without the Honda Insight is .963. This indicates that there is a strong linear relationship between the two variables. It is easy to see evidence of this relationship on the scatterplot. The Honda Insight should increase the correlation since it is in line with the pattern formed by the rest of the data. The correlation of all 22 vehicles is .981.

4.17

a) The correlation for the data in figure 4.6 is clearly positive but not near 1. There is a clear positive linear trend that can be seen in the scatterplot, but the points are not tightly clustered on a line, so the correlation will not be near 1.

b) The correlation for the data in figure 4.7 should be closer to 1 than the correlation for the data in figure 4.6. This is because there appears to be less spread away from the line that would pass through the data.

4.19 Removing the outliers from figure 4.6 will increase the correlation as they are pretty clearly not in line with the trend of the rest of the data. Removing the outliers from figure 4.7 may decrease the correlation since the one outlier is roughly along the same trend line as the rest of the data.

4.22

a) There should be a positive correlation between tail length and weight because tail length should be positively related with the body length of the rat. Rats with longer bodies will tend to be heavier than those with shorter bodies.

b) 9.8/2.54 = 3.86 inches.

c) The correlation would be 0.6 even if the length were in inches rather than centimeters.

4.27

a)

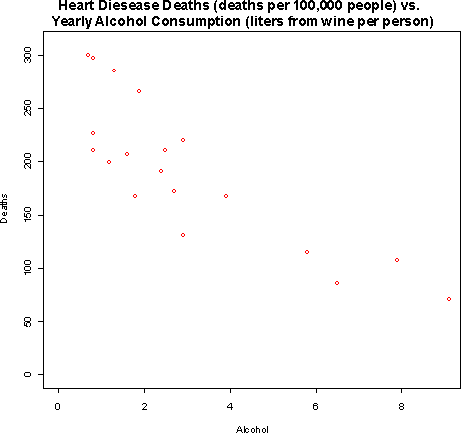
b)The relationship appears to be quite strong and more or less linear. Increased alcohol consumption from wine is associated with lower death rates due to heart disease.

c) The association is negative (increase alcohol is associated with decreased death rates). This data does not provide strong evidence that drinking wine causes a reduction in heart disease deaths. There could be lurking variables that are associated with both. For example, it may be that people who drink wine also tend to eat more fruits and vegetables.

4.30

a) Correlation cannot be calculated unless both variables are quantitative. Gender is categorical.

b) Correlation cannot be greater than 1.

c) Correlation is a unitless measure, so it does not make sense to have a correlation in bushels.